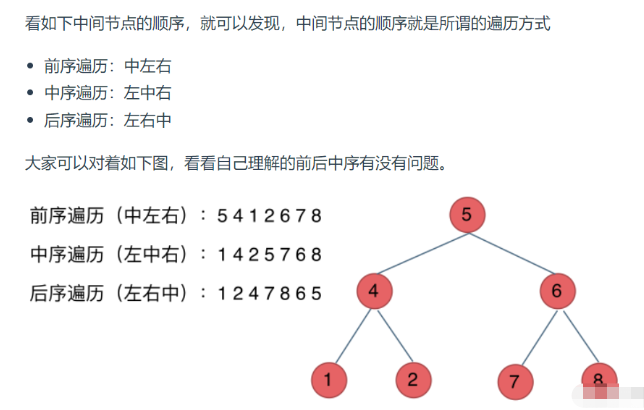
二叉树的遍历方法分为前序遍历,中序遍历,后续遍历,层序遍历。
对于递归,就不得不说递归三要素:以前序遍历为例
递归入参参数和返回值
因为要打印出前序遍历节点的数值,所以参数里需要传入List在放节点的数值,除了这一点就不需要在处理什么数据了也不需要有返回值,所以递归函数返回类型就是void,代码如下:
public void preorder(TreeNode root, List<Integer> result)
确定终止条件
在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点是空了,那么本层递归就要要结束了,所以如果当前遍历的这个节点是空,就直接return
if (root == null) return;
单层循环逻辑
前序遍历是中左右的循序,所以在单层递归的逻辑,是要先取中节点的数值,代码如下:
result.add(root.val); preorder(root.left, result); preorder(root.right, result);
// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);//先保存中间节点
preorder(root.left, result); //处理左边节点
preorder(root.right, result); //处理右边节点
}
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list); //先处理左边节点
list.add(root.val); //保存中间当前的节点
inorder(root.right, list);//先处理右边节点
}
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list); //先处理左边节点
postorder(root.right, list); //再处理右边节点
list.add(root.val); //保存最后
}
}//前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack();
if (root == null) return res;
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.right != null) { //先将右孩子入栈,因为它在最后
stack.push(node.right);
}
if (node.left != null) { //左孩子入栈再出栈
stack.push(node.left);
}
}
return res;
}
}
//中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
//如果可以,一直往左下探
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop(); //弹出来的肯定是叶子节点或中间节点
res.add(cur.val); //将这个节点加入list
cur = cur.right; //查看当前节点是否有右节点,如果右,肯定是中间节点,如果没有,就是叶子节点,继续弹出就可以
}
}
return res;
}
}
//后序遍历
//再来看后序遍历,先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.left != null) stack.push(node.left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
if (node.right != null) stack.push(node.right);// 空节点不入栈
}
Collections.reverse(res); // 将结果反转之后就是左右中的顺序了
return res;
}
}//前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}
//中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}
//后序遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
st.push(node); // 添加中节点
st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}





