在 m x n 的网格上有一个机器人。机器人最初位于左上角(即 grid[0][0])。机器人尝试移动到右下角(即 grid[m - 1][n - 1])。机器人在任何时间点只能向下或向右移动。
给定两个整数 m 和 n,返回机器人到达右下角可能采取的唯一路径的数量。
生成测试用例,以便答案将小于或等于 2 * 109。
示例1:
输入:m = 3,n = 7
输出:28
示例2:
输入:m = 3,n = 2
输出:3
说明:从左上角开始,到达右下角一共有3种方式:
限制:
1 <= m, n <= 100
原始页面
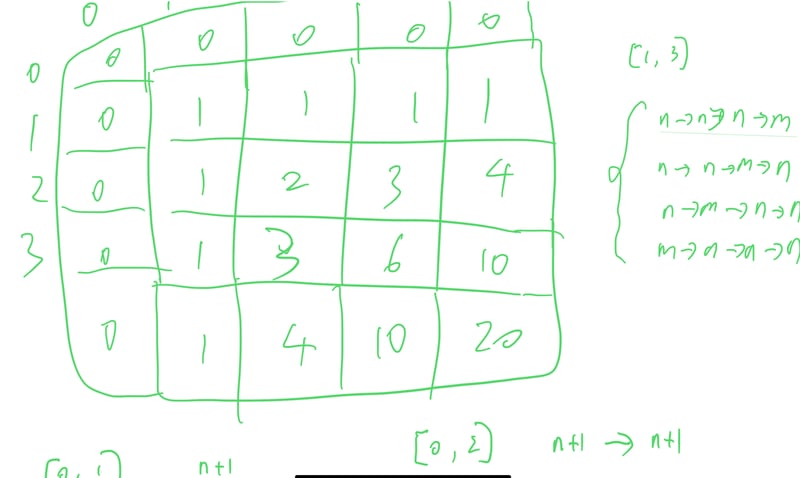
我们可以使用这个手写数组模拟来探索模式(顺便原谅我糟糕的笔迹)。
公共 int uniquePaths(int m, int n) {
if(n<=1 || m<=1){
返回1;
}
int dp[][] = new int[m+1][n+1];
dp[0][1] = 1;
for(int i=1; i
dp[0][1] = 1;对于这段代码,实际上我们使用 dp[1][0] = 1 还是 dp[0][1] = 1 并不重要,因为我们想要将索引匹配到 m 和 n,我们再扩展一行并当我们初始化数组时看到的列: int dp[][] = new int[m+1][n+1];
public int uniquePathsWithObstacles(int[][]barrierGrid) {
int row = 障碍网格.length;
int col = 障碍网格[0].length;
int[][] dp = new int[行][列];
布尔值 isBlocked = false;
for(int i=0; i<行; i++){
if(obstacleGrid[i][0]==1){
被阻止= true;
}
dp[i][0] = 被阻止? 0:1;
}
被阻止=假;
for(int i=0; i
没有什么特别难实现的,我们只需要考虑被遮挡的东西就可以了,但是很容易想到,这意味着当有被遮挡的东西时,无法通过被遮挡的东西左边或下方的格子这个方向。 (A格子的左边格子是被封锁的,我们无法从A的左边移动到A,只能找到向上的路线,这个逻辑也适用于向上)
343. 整数中断
给定一个整数 n,将其分解为 k 个正整数之和,其中 k >= 2,并最大化这些整数的乘积。
返回您可以获得的最大产品。
示例1:
输入:n = 2
输出:1
解释:2 = 1 + 1, 1 × 1 = 1.
示例2:
输入:n = 10
输出:36
解释:10 = 3 + 3 + 4, 3 × 3 × 4 = 36.
限制:
2 <= n <= 58
原始页面
公共 int integerBreak(int n) {
如果(n<=2){
返回1;
}
//在里面
int[] dp = 新 int[n+1];
dp[1] = 1;
dp[2] = 1;
//逻辑
for(int i=3; i<=n; i++){
for(int num=1; num





